Data
You will be redirected to cenamweb.org in 15 second(s). The JINA-CEE website is not updated anymore. The archived website can still be reached through the CeNAM website.
Stringent Constraints on Neutron-star Radii from Multimessenger Observations and Nuclear Theory

Neutron stars are the densest stellar objects that we can observe in the cosmos, and are arguably the most interesting astrophysical objects in the multimessenger era. The properties of gravitational waves, electromagnetic radiation, and neutrinos produced by a variety of neutron-star phenomena are determined by the nature of the matter that they contain. The nature of this matter holds important information needed to understand phases of matter encountered in Quantum Chromodynamics, and is described by the dense-matter equation of state (EOS). A measurement of the neutron-star radius or its compactness is critical both to interpret multimessenger observations of neutron stars and to determine EOS of dense matter [1]. A team of JINA-CEE researchers have now obtained the most stringent constraints on neutron-star radii to date by combining multimessenger observations of the fortuitously close binary neutron-star merger GW170817 [2] and its electromagnetic counterparts [3] with nuclear EOS constrained by chiral effective field theory, which best accounts for density-dependent uncertainties [4].
At low density, chiral effective field theory provides a description of matter in terms of nucleons and pions in which interactions are expanded in powers of momenta and include all operators consistent with the underlying symmetries of strong interactions [5]. This expansion defines a systematic order-by-order scheme that can be truncated at a given order and, most importantly, enables reliable theoretical uncertainty estimates from neglected contributions. Quantum Monte Carlo techniques are then used to solve the many-body Schrödinger equation to obtain the equation of state [6]. The resulting equation of state is characterized by an uncertainty which grows with density in a manner that can be justified from fundamental theory. To be conservative, we generate two collections of nuclear equations of state that differ in the density range restricted by ab initio calculations: chiral effective-field-theory constraints are either enforced up to nuclear saturation density or up to twice nuclear saturation density. We extend these equations of state to higher densities where the low-energy effective-field-theory expansion breaks down in a general way [4], while ensuring that the speed of sound is less than the speed of light and that the equations of state support a two-solar-mass neutron star.
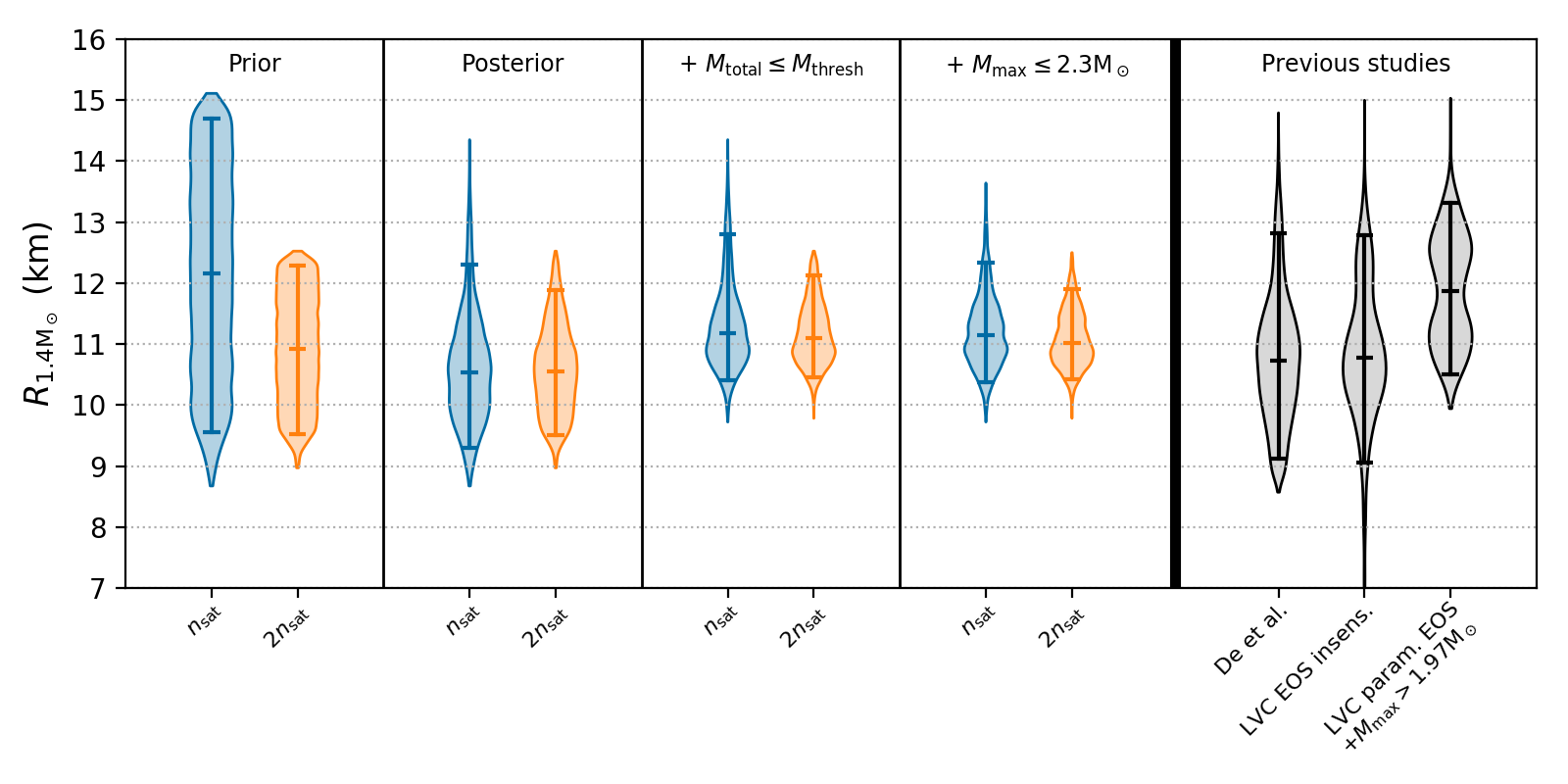
The multimessenger observations of GW170817 are then used to constrain these equations of state to ensure that they are consistent with: (i) the detected gravitational waves during the inspiral; (ii) the production of a post-merger remnant that does not immediately collapse to a black hole (BH); and (iii) the constraints that the energetics of the gamma-ray burst and kilonova place on the maximum mass of neutron stars. For each set of equations of state, we use stochastic samplers [7] to compute the posterior probability so that the tidal polarizability of GW170817 is consistent with a specific equation of state. Additional constraints on the equation of state can be obtained from the electromagnetic counterparts to GW170817. Since modeling the counterparts is challenging, we use a conservative approach that relies only on qualitative inferences from the kilonova and gamma-ray burst observations. The properties of these counterparts are inconsistent with either direct collapse to a black hole or the existence of a long-lived neutron-star remnant [8,9]. This allows us to place two further constraints on the equations of state. First, by discarding samples from the posterior in which the total gravitational mass of the binary exceeds the threshold for prompt collapse to a black hole. Secondly, by applying an upper limit on the maximum mass of neutron stars implied by the inconsistency of the electromagnetic counterparts with a long-lived neutron-star remnant [8]. Our results for the radius of a 1.4 Msol neutron star is shown at different stages in the analysis in Fig. 2. Using conservative assumptions on the nuclear physics and the properties of the electromagnetic counterpart, our analysis [10] showed that the radius of a 1.4 Msol neutron star is R1.4 =11 [+0.9,-0.6] km (4th panel in Fig. 2).
In their Nature Astronomy paper, the authors explore some of the implications of their findings, which are far reaching. For example, a kilonova or gamma-ray burst counterpart is only expected in a neutron star – black hole merger when the neutron star is tidally disrupted before the merger; a condition that depends crucially on the neutron-star radius. We have now shown that neutron stars are likely not disrupted in neutron-star black-hole mergers and that subsequently such events will not produce observable electromagnetic emission. Our improved constraints on the neutron-star radius also have implications for the interpretation of electromagnetic observations of neutron stars, in particular for X-ray observations of accreting neutron stars in low mass X-ray binaries (LMXBs), where the radius is a key parameter.
References:
[1] J.M. Lattimer, M. Prakash, Astrophys. J. 550, 426 (2001).
[2] B.P. Abbott et al., Phys. Rev. Lett. 119, 161101 (2017).
[3] B.P. Abbott et al., Astrophys. J. 848, L12 (2017).
[4] I. Tews, J. Margueron, and S. Reddy, Phys. Rev. C 98, 045804 (2018).
[5] S. Weinberg, Phys. Lett B251, 288 (1990) and Nucl. Phys B363 , 3 (1991).
[6] J. Carlson et al., Rev. Mod. Phys. 87, 1067 (2015).
[7] C. M. Biwer et al., Publ. Astron. Soc. Pac. 131, 024503 (2019).
[8] B. Margalit and B. D. Metzger, Astrophys. J. Lett. 850, L19 (2017).
[9] A. Bauswein, O. Just, H.-T. Janka, and N. Stergioulas, Astrophys. J. 850, L34 (2017).
[10] C.D. Capano et al., arXiv:1908.10352.
